К вопросу о математическом моделировании распределения воздуха в системах вентиляции зданий
Рассмотрены основные зависимости, описывающие взаимосвязь потерь давления и расхода воздуха в системах вентиляции зданий при математическом моделировании их воздушного режима. Предложены формулы, позволяющие с более высокой точностью учитывать характеристики вентиляторов, приточных, вытяжных клапанов и других элементов аэродинамической сети систем вентиляции. Проведена оценка влияния на результаты математического моделирования способа задания зависимости расхода воздуха от перепада давлений.
Математическое моделирование распределения потоков воздуха в системах вентиляции зданий является одним из основных методов прогнозирования их воздушного режима.Известен ряд работ, посвященных исследованию различных аспектов данного вопроса [1–9].
В общем случае постановка задачи сводится к представлению системы вентиляции здания в виде аэродинамической сети, состоящей из узлов (блоков), соединенных между собой связями, характеризующими сопротивление ограждающих конструкций, вентиляционных каналов, приточных или вытяжных решеток, клапанов и др. элементов. В узлах, под воздействием перепада давлений, поступает и удаляется определенное количество воздуха. При этом воздушный баланс каждого из узлов считается нулевым (количество поступившего воздуха равно ушедшему).
Движение воздуха по отдельным участкам аэродинамической сети принято описывать нелинейными уравнениями, отражающими взаимосвязь между перепадом давлений и расходом воздуха. Например, для вентиляционных каналов в большинстве работ применялась зависимость [1–8]
 (1)
(1)
где ΔPi – общая потеря давления на участке, Па1;
Gi – массовый расход воздуха на участке, кг/ч;
si – характеристика аэродинамического сопротивления участка, Па×ч2/кг2.
Для описания взаимосвязи движения воздуха через оконные блоки, в ряде работ [2–4] использовалось выражение типа
 (2)
(2)
или [6–8]
![]() (3)
(3)
где β – показатель степени, принимаемый в зависимости от режима течения воздуха через тот или иной элемент.
Задача моделирования воздухораспределения в системах вентиляции зданий сводится к составлению системы нелинейных уравнений типа (1)–(3) или их аналогов – по расчетной схеме системы вентиляции, и последующему решению системы уравнений с использованием различных математических методов. Известные методы – Ньютона, Зейделя, обобщенного приведенного градиента и др. [3–5]. Критериями решения являются допустимые невязки расходов воздуха, подходящих и уходящих от узлов, и перепады давлений в каждом независимом контуре схемы.
Сложность реализации изложенного подхода обусловлена тем, что перемещение воздуха через отдельные элементы рассматриваемой аэродинамической сети характеризуется разным режимом течения. Соответственно, для корректного описания зависимости между перепадом давления и расходом воздуха необходимо в каждом конкретном воздухопроницаемом элементе задавать математическую зависимость «давление – расход воздуха», определять величины характеристик сопротивлений si и показателей степени. Именно этим обусловлено применение различных формул, в той или иной мере уточняющих аппроксимацию зависимости «давление – расход воздуха».
При включении в аэродинамическую сеть вытяжных (или приточных) вентиляторов, появляется необходимость учета дополнительного давления Рвент, создаваемого вентиляторами на отдельных участках сети.
Например, уравнение (2) для i-го участка с вентилятором приобретает вид [2, 3]
 (4)
(4)
Вентилятор в данном случае рассматривается как источник давления, а не новый узел сети.
В работе [3] уравнение, описывающее работу вентилятора, предлагалось записывать в виде
 (5)
(5)
ρ – плотность воздуха, кг/м3;
Gi – массовый расход воздуха, кг/ч;
(Gi /ρ) – объемный расход воздуха, м3/ч.
Соответственно появляется задача определения и аппроксимации рабочих характеристик вентилятора Pвент = f(G) с последующим включением их в систему нелинейных уравнений.

Рис. 1. Характеристики некоторых индивидуальных вентиляторов (по данным заводов-изготовителей)
Следует отметить, что зависимости «давление – расход воздуха» для разных типов вентиляторов могут существенно отличаться и иметь различную форму (например, «седловидную»).
В современных системах вентиляции с применением приточных и вытяжных клапанов, изменяющих свои характеристики в зависимости от степени открытия регулирующей заслонки или положения ветрозащитной планки, задача моделирования воздушного режима зданий осложняется еще и необходимостью составления уравнений «давление – расход воздуха» для этих устройств, что в ряде случаев требует задания характеристик с переломными точками.
В качестве примера на рис. 2 приведены результаты испытаний оконного клапана «VentAir» с ветрозащитной планкой и варианты аппроксимации зависимости «давление – расход воздуха» по различным формулам (табл. 1).

Рис. 2. Результаты испытаний и аппроксимация зависимости «давление – расход воздуха» по различным формулам для оконного клапана «VentAir», полученные: 1 – по результатам испытаний; 2 – аппроксимацией по формуле (2); 3 – аппроксимацией по формуле (3); 4 – аппроксимацией по формуле (11) при степени аппроксимации k = 6
Следует отметить, что при расчете систем вентиляции с использованием ЭВМ в формулах (1)–(5) требовалось введение абсолютной величины Gi (по модулю). В результате вышеописанные формулы приобретали следующий вид:
 (6)
(6)
 (7)
(7)
 (8)
(8)
Введение модуля Gi указывало на то, что при отрицательных значениях расхода воздуха (случаи, когда направление движения противоположно заданному) движение воздуха будет определяться аналогичной зависимостью. В некоторых элементах аэродинамической сети (например, движение воздуха по вентиляционным каналам) данное условие справедливо, однако в ряде случаев, при изменении направления движения воздуха зависимость может изменяться. Простейший пример – обратный клапан, который при движении воздуха в обратном направлении закрывается и при любых перепадах давлений расход воздуха близок к нулю. Соответственно для полного описания работы элемента сети необходимо вводить в расчет несколько формул (одну в области отрицательных расходов, другую – в области положительных).
Расширение возможностей современных ЭВМ и совершенствование стандартных программных продуктов позволяет упростить подход к формированию систем нелинейных уравнений, обеспечить более точное и универсальное описание зависимостей «расход воздуха – потери давления».
Для этого предлагается использовать известную зависимость в виде алгебраического многочлена [5]
fi (xi) = si′·xi + si′′·xi2 + si ′′′·xi3..., (9)
Применительно к рассматриваемой задаче для i-го элемента вентиляционной сети можно записать
 (10)
(10)
или в общем виде
 (11)
(11)
В данном случае нет необходимости во введении модуля, так как аппроксимирующая функция позволяет описать значения расходов находящиеся как в положительной, так и в отрицательной областях (за исключением вентиляционных каналов и воздуховодов, для которых следует пользоваться формулой (6)).
Аналогичным образом предлагается описывать зависимость давления вентилятора от расхода, только в этом случае будет добавлен коэффициент s0, который соответствует максимальному давлению вентилятора:
![]() (12)
(12)
или в общем виде
 (13)
(13)
Применение формулы (13) позволяет вводить характеристику вентиляторов как в области отрицательных расходов (II квадрант), так и в области отрицательных давлений (IV квадрант).
Необходимо отметить, что во всех вышеперечисленных формулах используется массовый расход воздуха G, измеряемый в кг/ч. Однако в ряде задач более удобным является использование объемного расхода воздуха L, измеряемого в м3/ч и необходимо учитывать, что в этом случае коэффициенты si будут другими.
Результаты аппроксимации зависимостей «расход воздуха – перепад давлений» по формулам (11) и (13) для некоторых вентиляционных элементов приведены на рис. 2, 3 (табл. 1, 2).

Рис. 3. Результаты испытаний и аппроксимация зависимости «давление – расход воздуха» по различным формулам вентилятора MF 100/4” фирмы «Vortice»: 1 – результаты испытаний; 2 – аппроксимация по формуле (5); 3 – аппроксимация по предлагаемой формуле (13) при степени аппроксимации k = 6
В частности, описание характеристики приточных клапанов, полученное по формуле (11) ближе к фактической (см. рис. 2) по сравнению с кривыми, полученными по формулам (2, 3). Аналогичным образом могут отличаться и кривые, описывающие характеристики вентиляторов. В качестве примера на рисунке 3 представлена характеристика вентилятора MF 100/4” фирмы «Vortice».
В результате применение вышеописанных формул позволяет повысить точность расчета при моделировании воздушного режима здания.
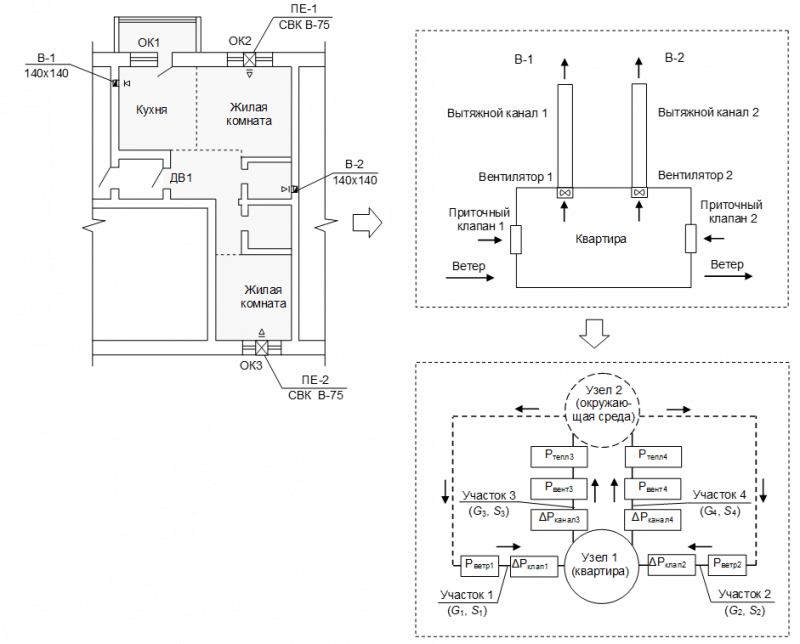
На рис. 4 приведена расчетная схема и граф системы вентиляции двухкомнатной квартиры верхнего этажа многоквартирного здания с вытяжными вентиляторами и приточными клапанами. Результаты расчета этой системы при аппроксимации зависимости Pвент = f(G) по формулам (5) и (13) представлены в табл. 3. Погрешность (расхождения в определении расходов воздуха) в приведенном примере составляет ~ 6-11%.

Рис. 4. Пример расчета воздухообмена двухкомнатной квартиры верхнего этажа многоквартирного жилого дома при аппроксимации Pвент по различным формулам
Экспериментальная проверка корректности предложенных зависимостей выполнена на лабораторном стенде, моделирующем сборный вытяжной канал с каналами-спутниками, в которые встроены осевые вентиляторы.
Общая схема стенда приведена в табл. 4. Диаметр сборного канала – 150 мм, диаметр каналов-спутников – 100 мм. Количество каналов-спутников – 4. Марка использованных вентиляторов – «Домовент 100».
Замеры расходов воздуха выполнялись с помощью анемометра «testo 417-2».
Следует отметить, что до начала испытаний были определены фактические характеристики вентиляторов «P–L» в соответствии с ГОСТ 10921–90 [10].
Результаты испытаний в сопоставлении с результатами расчетов, выполненных при аппроксимации характеристик вентиляторов по формуле (13), приведены в табл. 4.
Таблица 4
Результаты экспериментальной проверки предложенных зависимостей в лабораторных условиях

Заключение. Использование формул общего вида (11) и (13) обеспечивает универсальность подхода к аппроксимации зависимостей «расход воздуха – перепад давлений» для всех элементов аэродинамической сети и позволяет более точно определять расходы воздуха и потери давления при математическом моделировании воздушного режима здания.
Примечание:
1. Условные обозначения, использованные в разных литературных источниках, в данной статье приведены к единому виду.
Библиографический список
1. Гинзбург Э. Я. Расчет отопительно-вентиляционных систем с помощью ЭВМ. М.: Стройиздат, 1979.
2. Константинова В. Е. Расчеты воздухообмена в жилых и общественных зданиях. М.: Стройиздат, 1964.
3. Константинова В. Е. Воздушно-тепловой режим в жилых зданиях повышенной этажности. М.: Стройиздат, 1969.
4. Светлов К. С. Расчет воздухообмена в многоэтажных зданиях с использованием электронно-вычислительных машин // Водоснабжение и санитарная техника. 1966. № 11.
5. Меренков А. П., Хасилев В. Я. Теория гидравлических цепей. М.: Наука, 1985.
6. Кривошеин А. Д., Андреев И. В. Исследование процессов распределения воздуха в гибридных системах вентиляции жилых зданий // Вестник СибАДИ. 2013. №5 (33). С. 63–69.
7. Китайцева Е. Х. Обобщенные методы расчета воздушного режима здания и факторов, влияющих на качество внутреннего воздуха: автореф. дис. ... канд. техн. наук. М., 1995.
8. Бирюков С. В. Разработка метода определения нормы потребления тепловой энергии системами отопления и вентиляции общественных зданий: На примере учебных корпусов ВУЗов: дис. ... канд. техн. наук. М., 2002.
9. Бороздин Е. Г. Математическое описание работы вентиляторов в составе механических приточных устройств // Вестник СибАДИ. 2015. № 4 (44). С. 115–119.
10. ГОСТ 10921–90. Вентиляторы радиальные и осевые. Методы аэродинамических испытаний. Введ. 1992–01–01. М.: Госстандарт, 1992.
Pdf версия статьи, вышедшая в журнале "Омский научный вестник"
М.А. Кривошеин, к.т.н., директор ООО "ТЕХВЕНТ"
- Комментарии